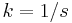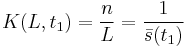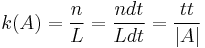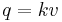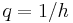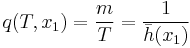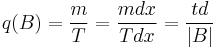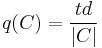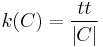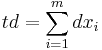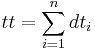Traffic flow
Traffic flow, in mathematics and civil engineering, is the study of interactions between vehicles, drivers, and infrastructure (including highways, signage, and traffic control devices), with the aim of understanding and developing an optimal road network with efficient movement of traffic and minimal traffic congestion problems.
Contents |
History
Attempts to produce a mathematical theory of traffic flow date back to the 1920s, when Frank Knight first produced an analysis of traffic equilibrium, which was refined into Wardrop's first and second principles of equilibrium in 1952.
Nonetheless, even with the advent of significant computer processing power, to date there has been no satisfactory general theory that can be consistently applied to real flow conditions. Current traffic models use a mixture of empirical and theoretical techniques. These models are then developed into traffic forecasts, to take account of proposed local or major changes, such as increased vehicle use, changes in land use or changes in mode of transport (with people moving from bus to train or car, for example), and to identify areas of congestion where the network needs to be adjusted.
Overview
Traffic phenomena are complex and nonlinear, depending on the interactions of a large number of vehicles. Due to the individual reactions of human drivers, vehicles do not interact simply following the laws of mechanics, but rather show phenomena of cluster formation and shock wave propagation, both forward and backward, depending on vehicle density in a given area. Some mathematical models in traffic flow make use of a vertical queue assumption, where the vehicles along a congested link do not spill back along the length of the link.
In a free flowing network, traffic flow theory refers to the traffic stream variables of speed, flow, and concentration. These relationships are mainly concerned with uninterrupted traffic flow, primarily found on freeways or expressways.[1] "Optimum density" for U.S. freeways is sometimes described as 40–50 vehicles per mile per lane. As the density reaches the maximum flow rate (or flux) and exceeds the optimum density, traffic flow becomes unstable, and even a minor incident can result in persistent stop-and-go driving conditions. The term jam density refers to extreme traffic density associated with completely stopped traffic flow, usually in the range of 185–250 vehicles per mile per lane.
However, calculations within congested networks are much more complex and rely more on empirical studies and extrapolations from actual road counts. Because these are often urban or suburban in nature, other factors (such as road-user safety and environmental considerations) also dictate the optimum conditions.
There are common spatiotemporal empirical features of traffic congestion that are qualitatively the same for different highways in different countries measured during years of traffic observations. Some of these common features of traffic congestion define synchronized flow and wide moving jam traffic phases of congested traffic in Kerner’s three-phase traffic theory of traffic flow.
Traffic stream properties
Traffic flow is generally constrained along a one-dimensional pathway (e.g. a travel lane). A time-space diagram provides a graphical depiction of the flow of vehicles along a pathway over time. Time is measured along the horizontal axis, and distance is measured along the vertical axis. Traffic flow in a time-space diagram is represented by the individual trajectory lines of individual vehicles. Vehicles following each other along a given travel lane will have parallel trajectories, and trajectories will cross when one vehicle passes another. Time-space diagrams are useful tools for displaying and analyzing the traffic flow characteristics of a given roadway segment over time (e.g. analyzing traffic flow congestion).
There are three main variables to visualize a traffic stream: speed (v), density (k), and flow (q).
Speed
Speed in traffic flow is defined as the distance covered per unit time.[2] The speed of every individual vehicle is almost impossible to track on a roadway; therefore, in practice, average speed is based on the sampling of vehicles over a period of time or area and is calculated and used in formulas. If speed is measured by keeping time as reference it is called time mean speed, and if it is measured by space reference it is called space mean speed.
- Time mean speed is measured by taking a reference area on the roadway over a fixed period of time. In practice, it is measured by the use of loop detectors. Loop detectors, when spread over a reference area, can record the signature of vehicles and can track the speed of each individual vehicle. However, average speed measurements obtained from this method are not accurate because instantaneous speeds averaged among several vehicles can not account for the difference in travel time for the vehicles that are traveling at different speeds over the same distance.
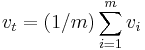 where m represents the number of vehicles passing the fixed point
where m represents the number of vehicles passing the fixed point
- Space mean speed is the speed measured by taking the whole roadway segment into account. Consecutive pictures or video of a roadway segment track the speed of individual vehicles, and then the average speed is calculated. It is considered more accurate than the time mean speed. The data for space calculating space mean speed may be taken from satellite pictures, a camera, or both.
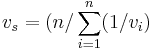 ) where n represents the number of vehicles passing the roadway segment
) where n represents the number of vehicles passing the roadway segment
The time mean speed is always greater than space mean speed.
In a time-space diagram, the instantaneous velocity, v = dx/dt, of a vehicle is equal to the slope along the vehicle’s trajectory. The average velocity of a vehicle is equal to the slope of the line connecting the trajectory endpoints where a vehicle enters and leaves the roadway segment. The vertical separation (distance) between parallel trajectories is the vehicle spacing (s) between a leading and following vehicle. Similarly, the horizontal separation (time) represents the vehicle headway (h). A time-space diagram is useful for relating headway and spacing to traffic flow and density, respectively.
Density
Density (k) is defined as the number of vehicles per unit area of the roadway. In traffic flow, the two most important densities are the critical density (kc) and jam density (kj). The maximum density achievable under free flow is kc, while kj is minimum density achieved under congestion. In general, jam density is seven times the critical density. Inverse of density is spacing (s), which is the distance between two vehicles.
The density (k) within a length of roadway (L) at a given time (t1) is equal to the inverse of the average spacing of the n vehicles.
In a time-space diagram, the density may be evaluated in the region A.
where tt is the total travel time in A
Flow
Flow (q) is the number of vehicles passing a reference point per unit of time, and is measured in vehicles per hour. The inverse of flow is headway (h), which is the time that elapses between the ith vehicle passing a reference point in space and the i+1 vehicle. In congestion, h remains constant. As a traffic jam forms, h approaches infinity.
The flow (q) passing a fixed point (x1) during an interval (T) is equal to the inverse of the average headway of the m vehicles.
In a time-space diagram, the flow may be evaluated in the region B.
where td is the total distance traveled in B.
Generalized Density and Flow in Time-Space Diagram
A more general definition of the flow and density in a time-space diagram is illustrated by region C:
where:
Congestion Shockwave
In addition to providing information on the speed, flow, and density of traffic streams, time-space diagrams may also illustrate the propagation of congestion upstream from a traffic bottleneck (shockwave). Congestion shockwaves will vary in propagation length, depending upon the upstream traffic flow and density. However, shockwaves will generally travel upstream at a rate of approximately 20 km/h.
Stationary traffic
We say that traffic on a long strech of road is stationary during a period of observation if you cannot get any clues as to what time it is or where you are by inspecting the time-space diagram through a small window in a template. Traffic is stationary if all the vehicles trajectories are paralel and equidistant. It is also stationare if it is a superposition of families of trajectories with these properties( eg. fast and slow drivers).Of course, by using a very small hole in the template one could sometimes view an empty region of the diagram and other times not, so that even in these cases, one could say that traffic was not stationary. Clearly, for such fine level of observation, stationary traffic does not exist. Obviously, we must exclude such a microscopic level of observation from the definition and must be satisfied if traffic appear to be similar through larger windows.in fact, we we relac the definition even further by only requiring that the quantities t(A) and d(A) are approximately the same; regardless of where the "large" window (A) is placed.
Methods of analysis
Scientists approach the problem in three main ways, corresponding to the three main scales of observation in physics.
- Microscopic scale: At the most basic level, every vehicle is considered as an individual. An equation can be written for each, usually an ordinary differential equation (ODE). Cellular automation models can also be used, where the road is discretised into cells which each contain a car moving with some speed, or are empty. The Nagel-Schreckenberg model is a simple example of a such a model. As the cars interact it can model collective phenomena such as traffic jams.
- Macroscopic scale: Similar to models of fluid dynamics, it is considered useful to employ a system of partial differential equations, which balance laws for some gross quantities of interest; e.g., the density of vehicles or their mean velocity.
- Mesoscopic (kinetic) scale: A third, intermediate possibility, is to define a function
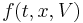 which expresses the probability of having a vehicle at time
which expresses the probability of having a vehicle at time  in position
in position  which runs with velocity
which runs with velocity  . This function, following methods of statistical mechanics, can be computed using an integro-differential equation, such as the Boltzmann equation.
. This function, following methods of statistical mechanics, can be computed using an integro-differential equation, such as the Boltzmann equation.
The engineering approach to analysis of highway traffic flow problems is primarily based on empirical analysis (i.e., observation and mathematical curve fitting). One of the major references on this topic used by American planners is the Highway Capacity Manual,[3] published by the Transportation Research Board, which is part of the United States National Academy of Sciences. This recommends modelling traffic flows using the whole travel time across a link using a delay/flow function, including the effects of queuing. This technique is used in many U.S. traffic models and the SATURN model in Europe.[4]
In many parts of Europe, a hybrid empirical approach to traffic design is used, combining macro-, micro-, and mesoscopic features. Rather than simulating a steady state of flow for a journey, transient "demand peaks" of congestion are simulated. These are modeled by using small "time slices" across the network throughout the working day or weekend. Typically, the origins and destinations for trips are first estimated and a traffic model is generated before being calibrated by comparing the mathematical model with observed counts of actual traffic flows, classified by type of vehicle. "Matrix estimation" is then applied to the model to achieve a better match to observed link counts before any changes, and the revised model is used to generate a more realistic traffic forecast for any proposed scheme. The model would be run several times (including a current baseline, an "average day" forecast based on a range of economic parameters and supported by sensitivity analysis) in order to understand the implications of temporary blockages or incidents around the network. From the models, it is possible to total the time taken for all drivers of different types of vehicle on the network and thus deduce average fuel consumption and emissions.
Much of UK, Scandinavian, and Dutch authority practice is to use the modelling program CONTRAM for large schemes, which has been developed over several decades under the auspices of the UK's Transport Research Laboratory, and more recently with the support of the Swedish Road Administration.[5] By modelling forecasts of the road network for several decades into the future, the economic benefits of changes to the road network can be calculated, using estimates for value of time and other parameters. The output of these models can then be fed into a cost-benefit analysis program.[6]
Cumulative vehicle count curves (N-curves)
A cumulative vehicle count curve, commonly known as the N-curve, is a curve that shows the cumulative number of vehicles that passes a certain location x by time t, measured from the passage of some reference vehicle[7]. This curve can be plotted if the arrival times are known for individual vehicles approaching a certain location x, and the departure times are also known as they leave location x. Obtaining these arrival and departure times could involve data collection: for example, one could set two point sensors at locations X1 and X2, and count the number of vehicles that pass through this segment while also recording the time each vehicle arrives at X1 and departs from X2. The resulting plot is a pair of cumulative curves where the vertical axis (N) represents the cumulative number of vehicles that passed the two points: X1 and X2, and the horizontal axis (t) represents the elapsed time from X1 and X2.
If vehicles experience no delay whatsoever as they travel from X1 to X2, then the arrivals of vehicles at location X1 is represented by curve N1 and the arrivals of the vehicles at location X2 is represented by N2 on Figure 8. More commonly, curve N1 is known as the arrival curve of vehicles at location X1 and curve N2 is known as the arrival curve of vehicles at location X2. Let’s take a one-lane signalized approach to an intersection as an example, where X1 is the location of the stop bar at the approach and X2 is an arbitrary line on the receiving lane just across of the intersection. When the traffic signal is green, vehicles can simply travel through both points with no delay and the time it takes to travel that distance is equal to the free-flow travel time. Graphically, this is shown as the two separate curves shown in Figure 8.
However, when the traffic signal is red, vehicles arrive at the stop bar (X1) and are delayed by the red light before finally crossing X2 some time after the signal turns green. In result, there is a queue that builds at the stop bar as more vehicles are arriving at the intersection while the traffic signal is still red. Therefore, for as long as vehicles arriving at the intersection are still hindered by the queue, the curve N2 no longer represents the vehicles’ arrival at location X2. Instead, the curve N2 now represents the vehicles’ virtual arrival at location X2, or in other words, it represents the vehicles' arrival at X2 if they did not experience any delay. The vehicles’ arrival at location X2, taking into account the delay from the traffic signal, is now represented by the curve N’2 on Figure 9.
However, the concept of the virtual arrival curve is flawed. This curve does not correctly show the queue length resulting from the interruption in traffic (i.e. red signal). In fact, it assumes that all vehicles are still reaching the stop bar before being delayed by the red light. In other words, the virtual arrival curve portrays the stacking of vehicles vertically at the stop bar. When the traffic signal turns green, these vehicles are served in a first-in-first-out (FIFO) order. For a multi-lane approach, however, the service order is not necessarily FIFO. Nonetheless, the interpretation is still useful because of the concern with average total delay instead of total delays for individual vehicles [8].
Step function vs. smooth function
The traffic light example depicts N-curves as smooth functions. Theoretically, however, plotting N-curves from collected data should result in a step-function (Figure 10). Each step represents the arrival or departure of one vehicle at that point in time [8]. When the N-curve is drawn on larger scale reflecting a period of time that covers several cycles, then the steps for individual vehicles can be ignored, and the curve will then look like a smooth function (Figure 8).
N-curve: traffic flow characteristics
The N-curve can be used in a number of different traffic analyses: including freeway bottlenecks and dynamic traffic assignment. This is due to the fact that a number of traffic flow characteristics can be derived from the plot of cumulative vehicle count curves. Illustrated in Figure 11 are the different traffic flow characteristics that can be derived from the N-curves.
These are the different traffic flow characteristics from Figure 11:
| Symbol | Definition |
|---|---|
| N1 | the cumulative number of vehicles arriving at location X1 |
| N2 | the virtual cumulative number of vehicles arriving at location X2, or the cumulative number of vehicles that would have liked to cross X2 by time t |
| N'2 | the actual cumulative number of vehicles arriving at location X2 |
| TTFF | the time it takes to travel from location X1 to location X2 at free-flow conditions |
| w(i) | the delay experienced by vehicle i as it travels from X1 to X2 |
| TT(i) | the total time it takes to travel from X1 to X2 including delays (TTFF + w(i)) |
| Q(t) | the queue at any time t, or the number of vehicles being delayed at time t |
| n | total number of vehicles in the system |
| m | total number of delayed vehicles |
| TD | total delay experienced by m vehicles (area between N2 and N'2) |
| t1 | time at which congestion begins |
| t2 | time at which congestion ends |
From these variables, the average delay experienced by each vehicle and the average queue length at any time t can also be calculated. These are calculated using the following formulas:
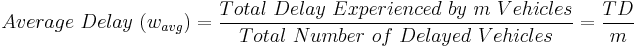
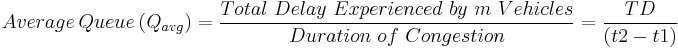
Applications
The bottleneck model
One application of the N-curve is the bottleneck model. In a bottleneck model, the cumulative vehicle count is known at a point before the bottleneck (i.e. this is location X1). However, the cumulative vehicle count is not known at a point after the bottleneck (i.e. this is location X2), but rather only the capacity of the bottleneck, or the discharge rate, μ, is known. The bottleneck model can be applied to real-world bottleneck situations such as those resulting from a roadway design problem or a traffic incident.
Take a roadway section where a bottleneck exists such as in Figure 12. At some location X1 before the bottleneck, the arrivals of vehicles follow a regular N-curve. If the bottleneck is absent, then the departure rate of vehicles at location X2 is essentially the same as the arrival rate at X1 at some time later (i.e. at time TTFF – free-flow travel time). However, due to the bottleneck, the system at location X2 is now only able to have a departure rate of μ. When graphing this scenario, essentially we have the same situation as in Figure 9: where the arrival curve of vehicles is N1, the departure curve of vehicles absent the bottleneck is N2, and the limited departure curve of vehicles given the bottleneck is N’2. The discharge rate μ is the slope of curve N’2, and all the same traffic flow characteristics as in Figure 11 can be determined from this diagram. The maximum delay and maximum queue length can be found at a point M on Figure 13 where the slope of N2 is the same as the slope of N’2, or in other words when the virtual arrival rate is equal to the discharge / departure rate μ.
Additional uses of the N-curve in the bottleneck model is that it is also able to calculate the benefits in removing the bottleneck, whether in terms of a capacity improvement or removing an incident to the side of the roadway.
Dynamic traffic assignment
Dynamic traffic assignment can also be solved using the N-curve. There are two main approaches to tackle this problem: System Optimum or User Optimum. This section will be discussed further in the following section.
Traffic assignment
The ultimate aim of traffic flow is to create and implement a model which would enable vehicles to reach their destination in the shortest possible time using the maximum roadway capacity. This is a four step process:
- Generation: In this step the program estimates how many trips would be generated. For this, the program needs the statistical data of residence areas by population, location of workplaces etc.
- Distribution: After generation it makes the different Origin-Destination (OD) pairs between the location found in step 1.
- Model Split/Mode Choice: The system has to decide how much percentage of the population would be split between the difference modes of available transport, e.g. cars, buses, rails, etc.
- Route Assignment: Finally, routes are assigned to the vehicles based on minimum criterion rules.
This cycle is repeated until the solution converges.
There are two main approaches to tackle this problem with the end objectives:
System optimum
System Optimum is based on the assumption that routes of all vehicles would be controlled by the system, and that rerouting would be based on maximum utilization of resources and minimum travel time. Hence, in a System Optimum routing algorithm, all routes between a given OD pair have the same marginal travel time. The method always gives a better routing solution, but it is difficult to implement. The system that controls traffic has the knowledge of roadway capacity, and so it can limit traffic before the road turns into a congestion state. The individuals in vehicles are without the knowledge of roadway capacity and when they would see free flow traffic ahead, they are not likely to follow system.
User equilibrium
The user optimum equilibrium assumes that every user chooses his or her own route towards his or her destination based on the travel time that will be consumed in different route options. The user will choose the route which will cost him or her the least time to reach the destination. The user optimum model is often used in simulating the impact on traffic assignment by highway bottlenecks. When the congestion occurs on highway, it will extend the delay time in travelling through the highway and create a longer travel time. Under the user optimum assumption, the users would choose to wait until the travel time using a certain freeway is equal to the travel time using city streets, and hence equilibrium is reached. This equilibrium is caller User Equilibrium or Nash Equilibrium.
The core principle of User Equilibrium is that all used routes between a given OD pair have the same travel time. An alternative route option is enabled to use when the actual travel time in the system has reached the free-flow travel time on that route.
For a highway user optimum model considering one alternative route, a typical process of traffic assignment is shown in Figure 15. When the traffic demand stays below the highway capacity, the delay time on highway stays zero. When the traffic demand exceeds the capacity, the queue of vehicle will appear on the highway and the delay time will begin to grow. A portion of users will turn to the city streets when the delay time reaches the difference between the free-flow travel time on highway and the free-flow travel time on city streets. It indicates that the users staying on the highway will spend as much travel time as the ones who turn to the city streets. At this stage, the travel time on both the highway and the alternative route stays same and constant. This situation may be ended when the demand falls below the road capacity, that is the travel time on highway begins to decrease and all the users will stay on the highway. The total of part area 1 and 3 represents the benefits by providing an alternative route. The total of area 4 and area 2 shows the total delay cost in the system, in which area 4 is the total delay occurs on the highway and area 2 is the extra delay by shifting traffic to city streets.
Time delay
Both User Optimum and System Optimum can be further subdivided into two categories on the basis of the approach of time delay taken for their solution:
- Predictive Time Delay
- Reactive Time Delay
Predictive time delay is based on the concept that the system or the user knows when the congestion point is reached or when the delay of the freeway would be equal to the delay on city streets, and the decision for route assignment is taken in time. On the other hand, reactive time delay is when the system or user waits to experience the point where the delay is observed and the diversion of routes is in reaction to that experience. Predictive delay gives significantly better results as compared to the reactive delay method.
Kerner’s network breakdown minimization (BM) principle
Kerner introduced an alternative approach to traffic assignment based on his network breakdown minimization (BM) principle. Rather than an explicit minimization of travel time that is the objective of System Optimum and User Equilibrium, the BM principle minimizes the probability of the occurrence of traffic congestion in a traffic network. Under a great enough traffic demand, the application of the BM principle should lead to implicit minimization of travel time in the network.
Variable speed limit assignment
This is an upcoming approach of eliminating shockwave and increasing safety for the vehicles. The concept is based on the fact that the risk of accident on a roadway increases with speed differential between the upstream and downstream vehicles. The two types of crash risk which can be reduced from VSL implementation are the rear end crash risk and the lane change crash risk. Different approaches have been implemented by researchers to build a suitable VSL algorithm.
Road junctions
A major consideration in road capacity relates to the design of junctions. By allowing long "weaving sections" on gently curving roads at graded intersections, vehicles can often move across lanes without causing significant interference to the flow. However, this is expensive and takes up a large amount of land, so other patterns are often used, particularly in urban or very rural areas. Most large models use crude simulations for intersections, but computer simulations are available to model specific sets of traffic lights, roundabouts, and other scenarios where flow is interrupted or shared with other types of road users or pedestrians. A well-designed junction can enable significantly more traffic flow at a range of traffic densities during the day. By matching such a model to an "Intelligent Transport System", traffic can be sent in uninterrupted "packets" of vehicles at predetermined speeds through a series of phased traffic lights. The UK's TRL has developed junction modelling programs for small-scale local schemes that can take account of detailed geometry and sight lines; ARCADY for roundabouts, PICADY for priority intersections, and OSCADY and TRANSYT for signals.
Traffic bottleneck
Stationary bottleneck
Consider a stretch of highway with two lanes in one direction. Suppose that the fundamental diagram is modeled as shown here. The highway has a peak capacity of Q vehicles per hour, corresponding to a density of kc vehicles per mile. The highway normally becomes jammed at kj vehicles per mile.
Before capacity is reached, traffic may flow at A vehicles per hour, or a higher B vehicles per hour. In either case, the speed of vehicles is vf, or "free flow," because the roadway is under capacity.
Now, suppose that at a certain location x0, the highway narrows to one lane. The maximum capacity is now limited to D', or half of Q, since only lane of the two is available. D shares the same flowrate as state D', but its vehicular density is higher.
Using a time-space diagram, we may model the bottleneck event. Suppose that at time 0, traffic begins to flow at rate B and speed vf. After time t1, vehicles arrive at the lighter flowrate A.
Before the first vehicles reach location x0, the traffic flow is unimpeded. However, downstream of x0, the roadway narrows, reducing the capacity by half - and to below that of state B. Due to this, vehicles will begin queuing upstream of x0. This is represented by high-density state D. The vehicle speed in this state is the slower vd, as taken from the fundamental diagram. Downstream of the bottleneck, vehicles transition to state D', where they again travel at free-flow speed vf.
Once vehicles arrive at rate A starting at t1, the queue will begin to clear and eventually dissipate. State A has a flowrate below the one-lane capacity of states D and D'.
On the time-space diagram, a sample vehicle trajectory is represented with a dotted arrow line. The diagram can readily represent vehicular delay and queue length. It's a simple matter of taking horizontal and vertical measurements within the region of state D.
Moving bottleneck
For this example, consider three lanes of traffic in one direction. Assume that a truck starts traveling at speed v, slower than the free flow speed vf. As shown on the fundamental diagram below, qu represents the reduced capacity (2/3 of Q, or 2 of 3 lanes available) around the truck.
State A represents normal approaching traffic flow, again at speed vf. State U, with flowrate qu, corresponds to the queuing upstream of the truck. On the fundamental diagram, vehicle speed vu is slower than vf. But once drivers have navigated around the truck, they can again speed up and transition to downstream state D. While this state travels at free flow, the vehicle density is less because fewer vehicles get around the bottleneck.
Suppose that, at time t, the truck slows from free-flow to v. A queue builds behind the truck, represented by state U. Within the region of state U, vehicles drive slower as indicated by the sample trajectory. Because state U limits to a smaller flow than state A, the queue will back up behind the truck and eventually crowd out the entire highway (slope s is negative). If state U had the higher flow, there would still be a growing queue. However, it would not back up because the slope s would be positive.
See also
- Data flow
- Dijkstra's algorithm
- Flow (computer networking)
- Fundamental diagram of traffic flow
- Journal of Transport and Land Use
- Microscopic traffic flow model
- Microsimulation
- Newell's Car Following Model
- Newell-Daganzo Merge Model
- Truck Lane Restriction
- Road traffic control
- Rule 184
- Three-phase traffic theory
- Three-detector problem and Newell's method
- TIRTL
- Traffic bottleneck
- Traffic wave
- Traffic counter
- Traffic congestion: Reconstruction with Kerner’s three-phase theory
- Turning movement counters
References
- ^ Henry Lieu (January/February 1999·). "Traffic-Flow Theory". Public Roads (US Dept of Transportation) (Vol. 62· No. 4). http://www.fhwa.dot.gov/publications/research/operations/tft/index.cfm.
- ^ Ergotmc @ GTRI Georgia Tech http://ergotmc.gtri.gatech.edu/
- ^ Highway Capacity Manual 2000
- ^ SATURN ITS Transport Software Site
- ^ Introduction to Contram
- ^ UK Department for Transport's WebTag guidance on the conduct of transport studies
- ^ Cassidy, M.J. and R.L. Bertini. "Some Traffic Features at Freeway Bottlenecks." Transportation Research Part B: Methodological 33.1 (1999) : 25-42.
- ^ a b Pitstick, Mark E. "Measuring Delay and Simulating Performance at Isolated Signalized Intersections Using Cumulative Curves." Transportation Research Record 1287 (1990).
Further reading
A survey about the state of art in traffic flow modelling:
- N. Bellomo, V. Coscia, M. Delitala, On the Mathematical Theory of Vehicular Traffic Flow I. Fluid Dynamic and Kinetic Modelling, Math. Mod. Meth. App. Sc., Vol. 12, No. 12 (2002) 1801–1843
- S. Maerivoet, Modelling Traffic on Motorways: State-of-the-Art, Numerical Data Analysis, and Dynamic Traffic Assignment, Katholieke Universiteit Leuven, 2006
- M. Garavello and B. Piccoli, Traffic Flow on Networks, American Institute of Mathematical Sciences (AIMS), Springfield, MO, 2006. pp xvi+243 ISBN 978-1-60133-000-0
- Carlos F.Daganzo, "Fundamentals of Transportation and Traffic Operations.",Pergamon-Elsevier, Oxford, U.K. (1997)
- B.S. Kerner, Introduction to Modern Traffic Flow Theory and Control: The Long Road to Three-Phase Traffic Theory, Springer, Berlin, New York 2009
- Cassidy, M.J. and R.L. Bertini. "Observations at a Freeway Bottleneck." Transportation and Traffic Theory (1999).
- Daganzo, Carlos F. "A Simple Traffic Analysis Procedure." Networks and Spatial Economics 1.i (2001) : 77-101.
- Lindgren, Robert V.R. "Analysis of Flow Features in Queued Traffic on a German Freeway." Portland State University (2005).
- Ni, B. and J.D. Leonard. "Direct Methods of Determining Traffic Stream Characteristics by Definition." Transportation Research Record (2006).
Useful books from the physical point of view:
- B.S. Kerner, The Physics of Traffic, Springer, Berlin, New York 2004
- Traffic flow on arxiv.org
- May, Adolf. Traffic Flow Fundamentals. Prentice Hall, Englewood Cliffs, NJ, 1990.
- Taylor, Nicholas. The Contram dynamic traffic assignment model TRL 2003